Fair share constraint resolution

In a retail supply materials are normally allocated in a proportional way. When only 100 units of supply are available when the forecasted demand is 200, you want to generate a plan where each customer receives a partial delivery of the forecasted demand.

This is different from detailed scheduling in a production environment. In such an environment you will typically plan to meet the most urgent and critical customer orders first, and delay the delivery of less important customer orders.

Check this feature on a live example

Download an Excel spreadsheet with the data for this example

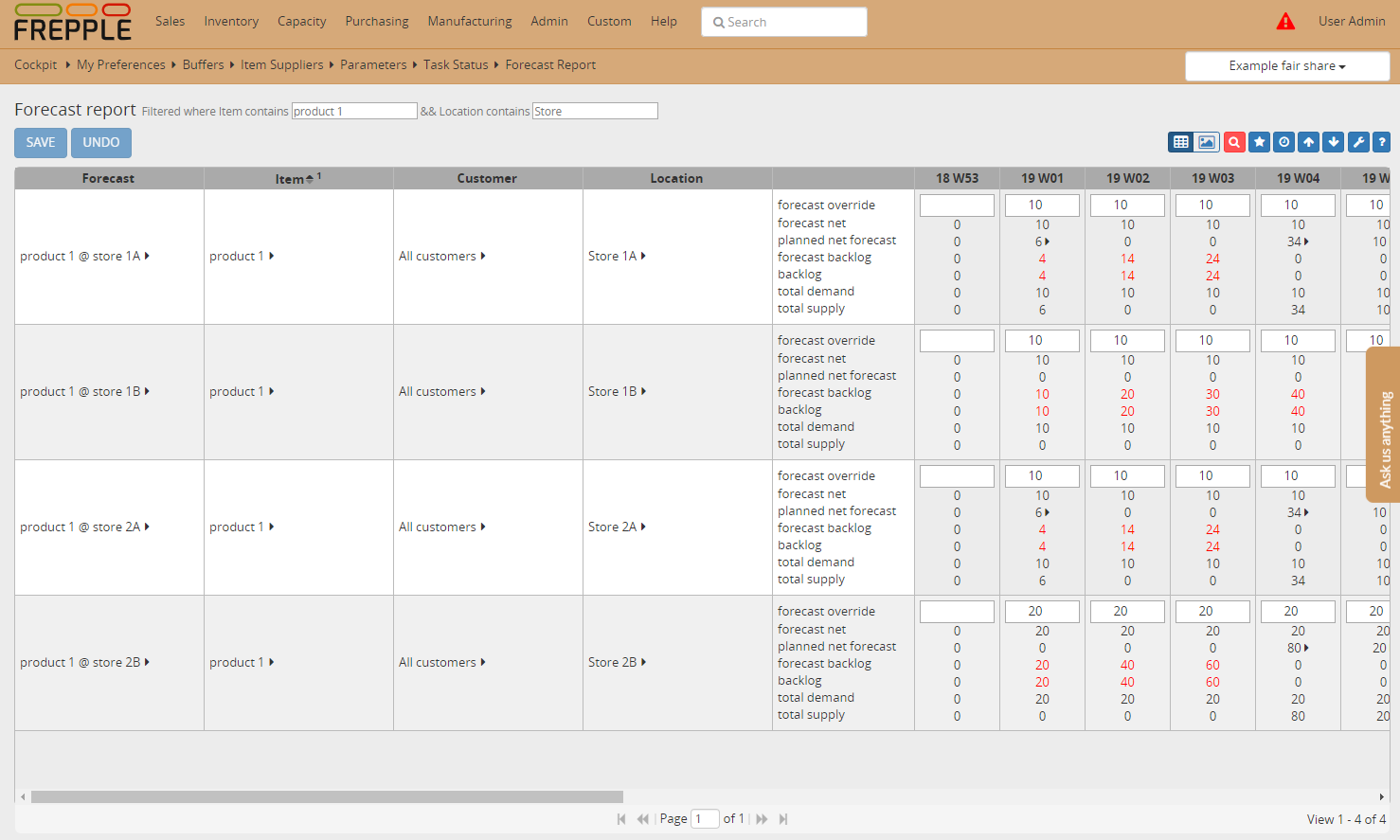
In this example we demonstrate the allocation of constrained supply among 2 stores.

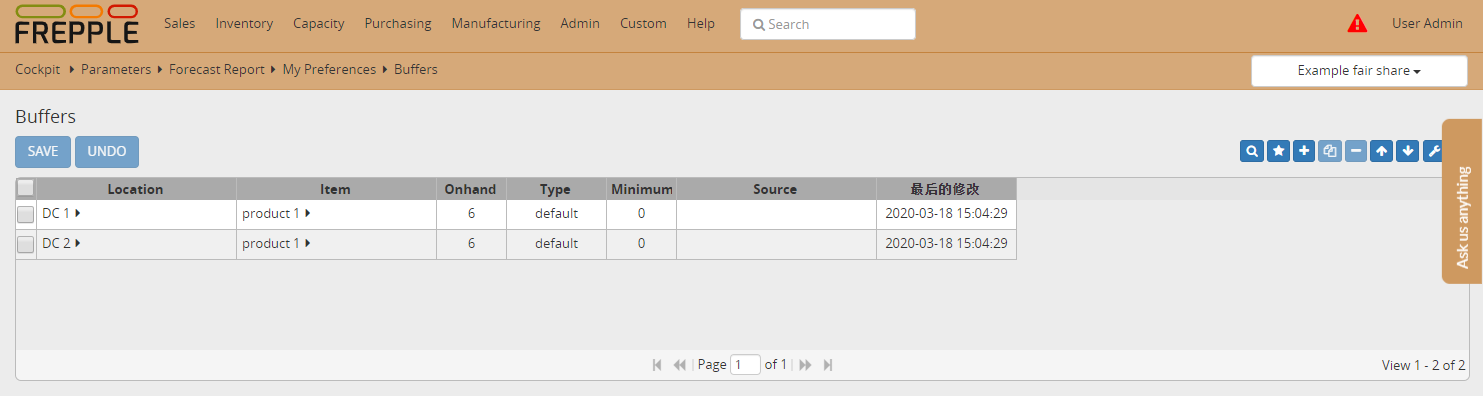
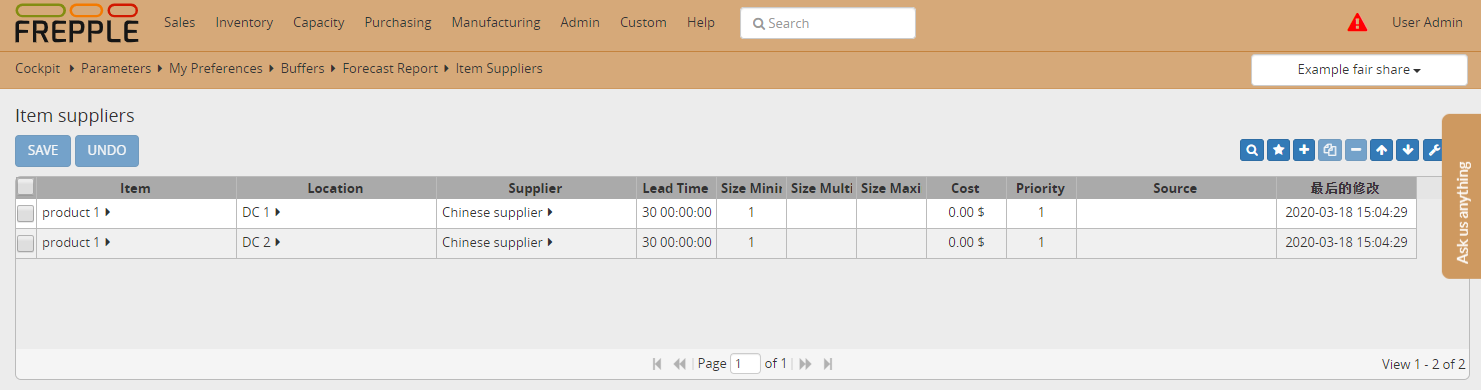
• In this example the available on hand inventory of “product 1” is only 6 units in each of the distribution centers.
  The supplier lead time is 30 days in each distribution center.
  With a weekly forecast of 10 units in each store, we are clearly in a shortage situation for the next 30 days.
  
• You can review the allocation of the supply during the shortage period in the forecast report Each store gets an allocation that is proportional to its forecasted sales.
  The 6 units that are available in “DC 1” are distributed 50% - 50% over “store 1A” and “store 1B”.
  The 6 units that are available in “DC 2” are distributed 33% - 66% over “store 2A” and “store 2B”.
  Notice also how the shortage ends after 30 months.
  
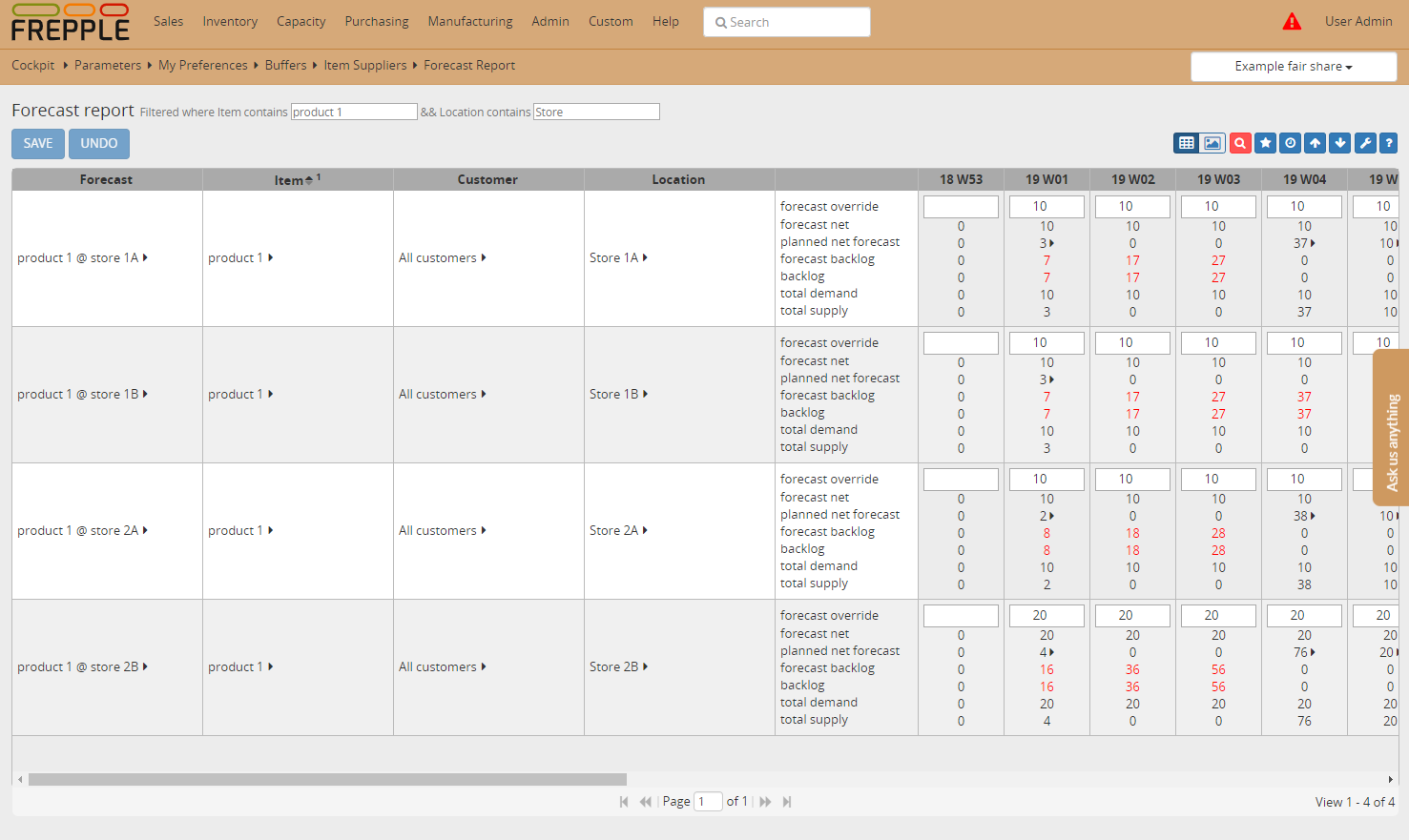
• The fair share allocation logic is only used when the parameter “plan.solver” has the value “distribution”. This activates a solver designed for solving distribution networks. (Do NOT use this solver on models with complex bill of materials and capacity constraints!)
  When the parameter “plan.solver” at its default value “heuristic”, we can see that the available inventory of 6 units is allocated in “first-come-first-served” mode to store 1A. Demand in store 1B only satisfied after the purchasing lead time.